A modeling averaging ensemble combines the prediction from each model equally and often results in better performance on average than a given single model.
Sometimes there are very good models that we wish to contribute more to an ensemble prediction, and perhaps less skillful models that may be useful but should contribute less to an ensemble prediction. A weighted average ensemble is an approach that allows multiple models to contribute to a prediction in proportion to their trust or estimated performance.
In this tutorial, you will discover how to develop a weighted average ensemble of deep learning neural network models in Python with Keras.
After completing this tutorial, you will know:
- Model averaging ensembles are limited because they require that each ensemble member contribute equally to predictions.
- Weighted average ensembles allow the contribution of each ensemble member to a prediction to be weighted proportionally to the trust or performance of the member on a holdout dataset.
- How to implement a weighted average ensemble in Keras and compare results to a model averaging ensemble and standalone models.
Let’s get started.

How to Develop a Weighted Average Ensemble for Deep Learning Neural Networks
Photo by Simon Matzinger, some rights reserved.
Tutorial Overview
This tutorial is divided into six parts; they are:
- Weighted Average Ensemble
- Multi-Class Classification Problem
- Multilayer Perceptron Model
- Model Averaging Ensemble
- Grid Search Weighted Average Ensemble
- Optimized Weighted Average Ensemble
Weighted Average Ensemble
Model averaging is an approach to ensemble learning where each ensemble member contributes an equal amount to the final prediction.
In the case of regression, the ensemble prediction is calculated as the average of the member predictions. In the case of predicting a class label, the prediction is calculated as the mode of the member predictions. In the case of predicting a class probability, the prediction can be calculated as the argmax of the summed probabilities for each class label.
A limitation of this approach is that each model has an equal contribution to the final prediction made by the ensemble. There is a requirement that all ensemble members have skill as compared to random chance, although some models are known to perform much better or much worse than other models.
A weighted ensemble is an extension of a model averaging ensemble where the contribution of each member to the final prediction is weighted by the performance of the model.
The model weights are small positive values and the sum of all weights equals one, allowing the weights to indicate the percentage of trust or expected performance from each model.
One can think of the weight Wk as the belief in predictor k and we therefore constrain the weights to be positive and sum to one.
— Learning with ensembles: How over-fitting can be useful, 1996.
Uniform values for the weights (e.g. 1/k where k is the number of ensemble members) means that the weighted ensemble acts as a simple averaging ensemble. There is no analytical solution to finding the weights (we cannot calculate them); instead, the value for the weights can be estimated using either the training dataset or a holdout validation dataset.
Finding the weights using the same training set used to fit the ensemble members will likely result in an overfit model. A more robust approach is to use a holdout validation dataset unseen by the ensemble members during training.
The simplest, perhaps most exhaustive approach would be to grid search weight values between 0 and 1 for each ensemble member. Alternately, an optimization procedure such as a linear solver or gradient descent optimization can be used to estimate the weights using a unit norm weight constraint to ensure that the vector of weights sum to one.
Unless the holdout validation dataset is large and representative, a weighted ensemble has an opportunity to overfit as compared to a simple averaging ensemble.
A simple alternative to adding more weight to a given model without calculating explicit weight coefficients is to add a given model more than once to the ensemble. Although less flexible, it allows a given well-performing model to contribute more than once to a given prediction made by the ensemble.
Want Better Results with Deep Learning?
Take my free 7-day email crash course now (with sample code).
Click to sign-up and also get a free PDF Ebook version of the course.
Multi-Class Classification Problem
We will use a small multi-class classification problem as the basis to demonstrate the weighted averaging ensemble.
The scikit-learn class provides the make_blobs() function that can be used to create a multi-class classification problem with the prescribed number of samples, input variables, classes, and variance of samples within a class.
The problem has two input variables (to represent the x and y coordinates of the points) and a standard deviation of 2.0 for points within each group. We will use the same random state (seed for the pseudorandom number generator) to ensure that we always get the same data points.
# generate 2d classification dataset X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
The results are the input and output elements of a dataset that we can model.
In order to get a feeling for the complexity of the problem, we can plot each point on a two-dimensional scatter plot and color each point by class value.
The complete example is listed below.
# scatter plot of blobs dataset
from sklearn.datasets.samples_generator import make_blobs
from matplotlib import pyplot
from pandas import DataFrame
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# scatter plot, dots colored by class value
df = DataFrame(dict(x=X[:,0], y=X[:,1], label=y))
colors = {0:'red', 1:'blue', 2:'green'}
fig, ax = pyplot.subplots()
grouped = df.groupby('label')
for key, group in grouped:
group.plot(ax=ax, kind='scatter', x='x', y='y', label=key, color=colors[key])
pyplot.show()
Running the example creates a scatter plot of the entire dataset. We can see that the standard deviation of 2.0 means that the classes are not linearly separable (separable by a line) causing many ambiguous points.
This is desirable as it means that the problem is non-trivial and will allow a neural network model to find many different “good enough” candidate solutions resulting in a high variance.
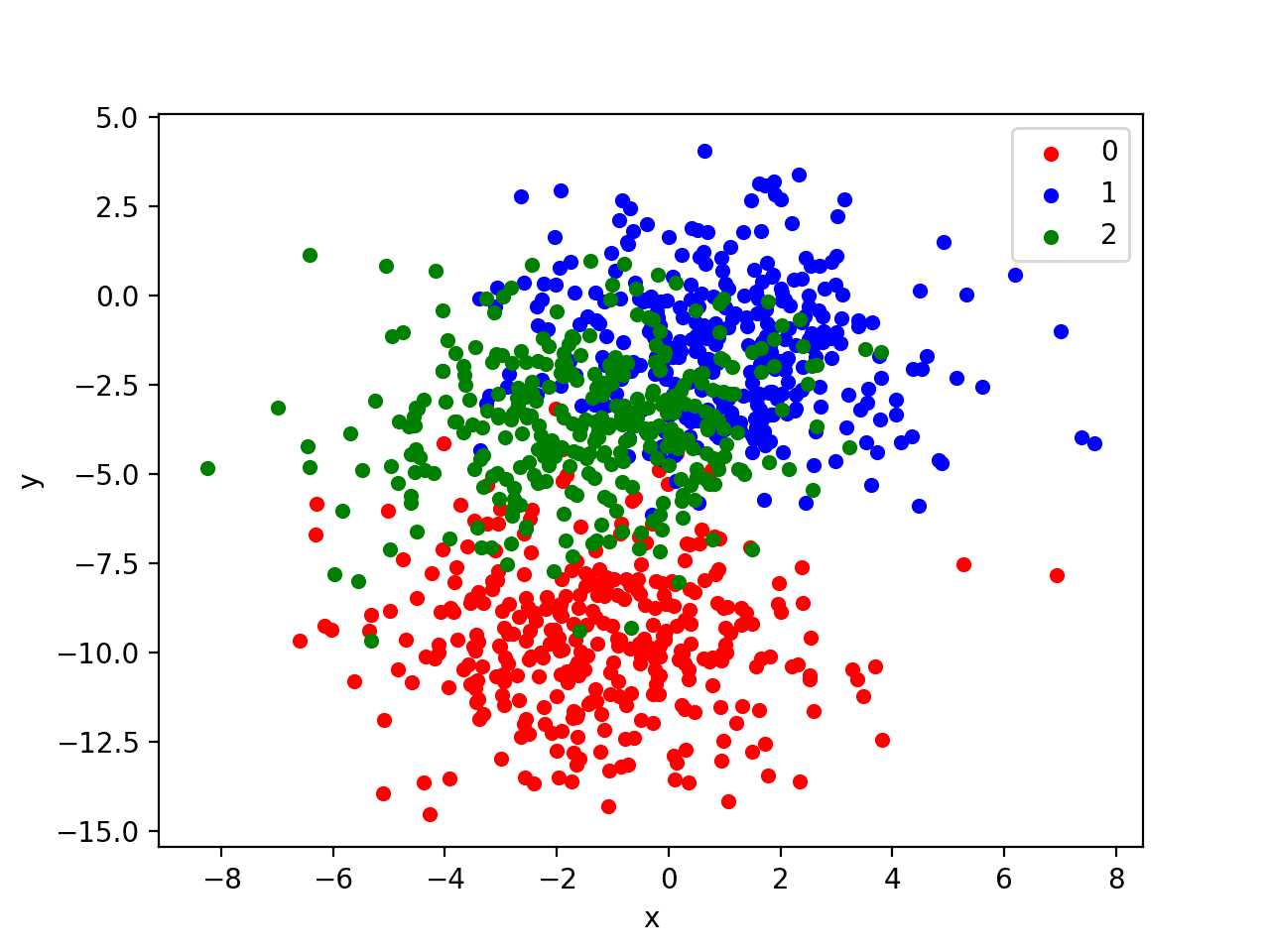
Scatter Plot of Blobs Dataset With Three Classes and Points Colored by Class Value
Multilayer Perceptron Model
Before we define a model, we need to contrive a problem that is appropriate for the weighted average ensemble.
In our problem, the training dataset is relatively small. Specifically, there is a 10:1 ratio of examples in the training dataset to the holdout dataset. This mimics a situation where we may have a vast number of unlabeled examples and a small number of labeled examples with which to train a model.
We will create 1,100 data points from the blobs problem. The model will be trained on the first 100 points and the remaining 1,000 will be held back in a test dataset, unavailable to the model.
The problem is a multi-class classification problem, and we will model it using a softmax activation function on the output layer. This means that the model will predict a vector with three elements with the probability that the sample belongs to each of the three classes. Therefore, we must one hot encode the class values before we split the rows into the train and test datasets. We can do this using the Keras to_categorical() function.
# generate 2d classification dataset X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2) # one hot encode output variable y = to_categorical(y) # split into train and test n_train = 100 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] print(trainX.shape, testX.shape)
Next, we can define and compile the model.
The model will expect samples with two input variables. The model then has a single hidden layer with 25 nodes and a rectified linear activation function, then an output layer with three nodes to predict the probability of each of the three classes and a softmax activation function.
Because the problem is multi-class, we will use the categorical cross entropy loss function to optimize the model and the efficient Adam flavor of stochastic gradient descent.
# define model model = Sequential() model.add(Dense(25, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
The model is fit for 500 training epochs and we will evaluate the model each epoch on the test set, using the test set as a validation set.
# fit model history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0)
At the end of the run, we will evaluate the performance of the model on the train and test sets.
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
Then finally, we will plot learning curves of the model accuracy over each training epoch on both the training and validation datasets.
# learning curves of model accuracy pyplot.plot(history.history['acc'], label='train') pyplot.plot(history.history['val_acc'], label='test') pyplot.legend() pyplot.show()
Tying all of this together, the complete example is listed below.
# develop an mlp for blobs dataset
from sklearn.datasets.samples_generator import make_blobs
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2)
# one hot encode output variable
y = to_categorical(y)
# split into train and test
n_train = 100
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
print(trainX.shape, testX.shape)
# define model
model = Sequential()
model.add(Dense(25, input_dim=2, activation='relu'))
model.add(Dense(3, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# learning curves of model accuracy
pyplot.plot(history.history['acc'], label='train')
pyplot.plot(history.history['val_acc'], label='test')
pyplot.legend()
pyplot.show()
Running the example first prints the shape of each dataset for confirmation, then the performance of the final model on the train and test datasets.
Your specific results will vary (by design!) given the high variance nature of the model.
In this case, we can see that the model achieved about 87% accuracy on the training dataset, which we know is optimistic, and about 81% on the test dataset, which we would expect to be more realistic.
(100, 2) (1000, 2) Train: 0.870, Test: 0.814
A line plot is also created showing the learning curves for the model accuracy on the train and test sets over each training epoch.
We can see that training accuracy is more optimistic over most of the run as we also noted with the final scores.
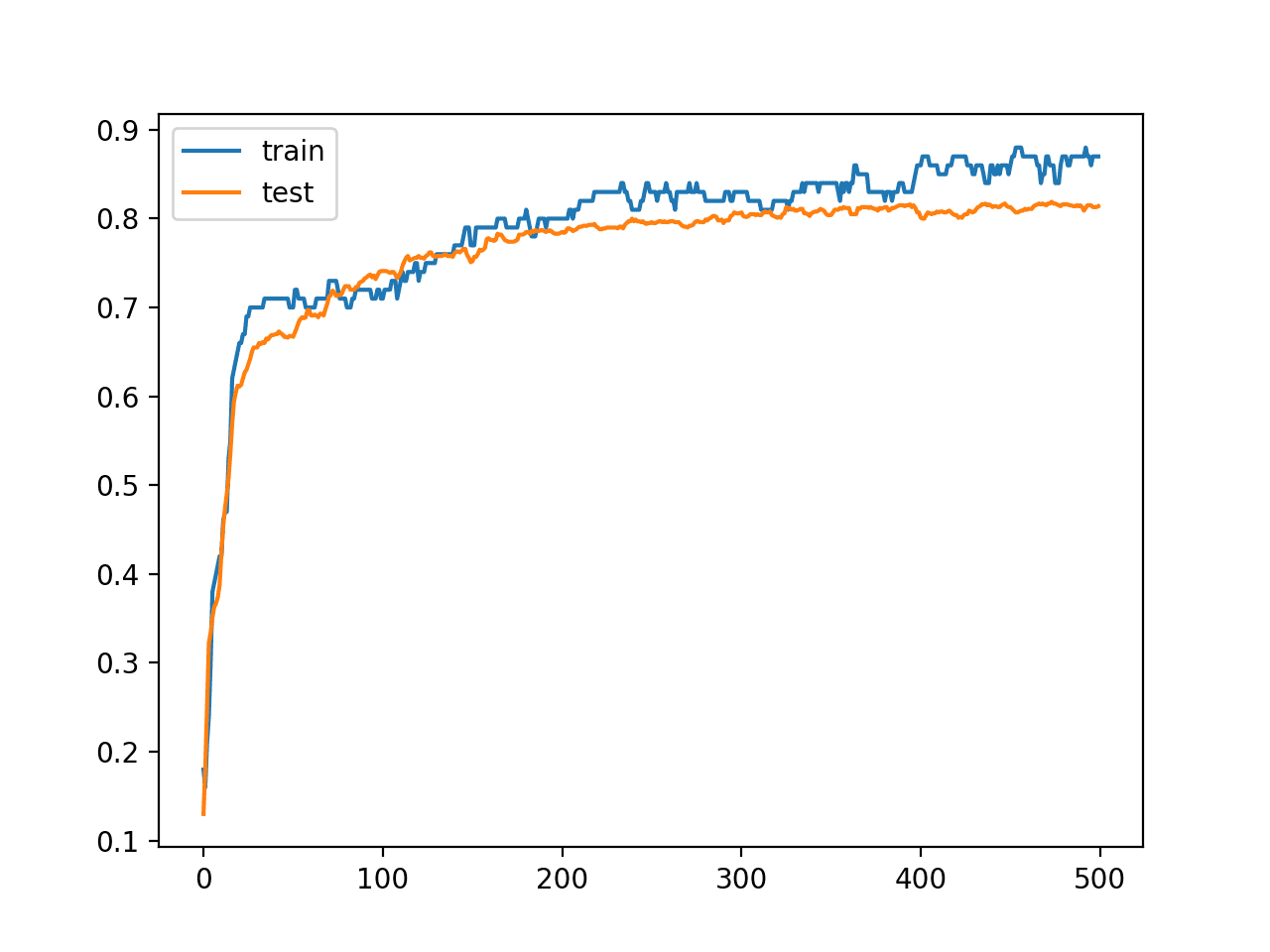
Line Plot Learning Curves of Model Accuracy on Train and Test Dataset over Each Training Epoch
Now that we have identified that the model is a good candidate for developing an ensemble, we can next look at developing a simple model averaging ensemble.
Model Averaging Ensemble
We can develop a simple model averaging ensemble before we look at developing a weighted average ensemble.
The results of the model averaging ensemble can be used as a point of comparison as we would expect a well configured weighted average ensemble to perform better.
First, we need to fit multiple models from which to develop an ensemble. We will define a function named fit_model() to create and fit a single model on the training dataset that we can call repeatedly to create as many models as we wish.
# fit model on dataset
def fit_model(trainX, trainy):
trainy_enc = to_categorical(trainy)
# define model
model = Sequential()
model.add(Dense(25, input_dim=2, activation='relu'))
model.add(Dense(3, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
model.fit(trainX, trainy_enc, epochs=500, verbose=0)
return model
We can call this function to create a pool of 10 models.
# fit all models n_members = 10 members = [fit_model(trainX, trainy) for _ in range(n_members)]
Next, we can develop model averaging ensemble.
We don’t know how many members would be appropriate for this problem, so we can create ensembles with different sizes from one to 10 members and evaluate the performance of each on the test set.
We can also evaluate the performance of each standalone model in the performance on the test set. This provides a useful point of comparison for the model averaging ensemble, as we expect that the ensemble will out-perform a randomly selected single model on average.
Each model predicts the probabilities for each class label, e.g. has three outputs. A single prediction can be converted to a class label by using the argmax() function on the predicted probabilities, e.g. return the index in the prediction with the largest probability value. We can ensemble the predictions from multiple models by summing the probabilities for each class prediction and using the argmax() on the result. The ensemble_predictions() function below implements this behavior.
# make an ensemble prediction for multi-class classification
def ensemble_predictions(members, testX):
# make predictions
yhats = [model.predict(testX) for model in members]
yhats = array(yhats)
# sum across ensemble members
summed = numpy.sum(yhats, axis=0)
# argmax across classes
result = argmax(summed, axis=1)
return result
We can estimate the performance of an ensemble of a given size by selecting the required number of models from the list of all models, calling the ensemble_predictions() function to make a prediction, then calculating the accuracy of the prediction by comparing it to the true values. The evaluate_n_members() function below implements this behavior.
# evaluate a specific number of members in an ensemble
def evaluate_n_members(members, n_members, testX, testy):
# select a subset of members
subset = members[:n_members]
# make prediction
yhat = ensemble_predictions(subset, testX)
# calculate accuracy
return accuracy_score(testy, yhat)
The scores of the ensembles of each size can be stored to be plotted later, and the scores for each individual model are collected and the average performance reported.
# evaluate different numbers of ensembles on hold out set
single_scores, ensemble_scores = list(), list()
for i in range(1, len(members)+1):
# evaluate model with i members
ensemble_score = evaluate_n_members(members, i, testX, testy)
# evaluate the i'th model standalone
testy_enc = to_categorical(testy)
_, single_score = members[i-1].evaluate(testX, testy_enc, verbose=0)
# summarize this step
print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score))
ensemble_scores.append(ensemble_score)
single_scores.append(single_score)
# summarize average accuracy of a single final model
print('Accuracy %.3f (%.3f)' % (mean(single_scores), std(single_scores)))
Finally, we create a graph that shows the accuracy of each individual model (blue dots) and the performance of the model averaging ensemble as the number of members is increased from one to 10 members (orange line).
Tying all of this together, the complete example is listed below.
# model averaging ensemble for the blobs dataset
from sklearn.datasets.samples_generator import make_blobs
from sklearn.metrics import accuracy_score
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense
from matplotlib import pyplot
from numpy import mean
from numpy import std
import numpy
from numpy import array
from numpy import argmax
# fit model on dataset
def fit_model(trainX, trainy):
trainy_enc = to_categorical(trainy)
# define model
model = Sequential()
model.add(Dense(25, input_dim=2, activation='relu'))
model.add(Dense(3, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
model.fit(trainX, trainy_enc, epochs=500, verbose=0)
return model
# make an ensemble prediction for multi-class classification
def ensemble_predictions(members, testX):
# make predictions
yhats = [model.predict(testX) for model in members]
yhats = array(yhats)
# sum across ensemble members
summed = numpy.sum(yhats, axis=0)
# argmax across classes
result = argmax(summed, axis=1)
return result
# evaluate a specific number of members in an ensemble
def evaluate_n_members(members, n_members, testX, testy):
# select a subset of members
subset = members[:n_members]
# make prediction
yhat = ensemble_predictions(subset, testX)
# calculate accuracy
return accuracy_score(testy, yhat)
# generate 2d classification dataset
X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2)
# split into train and test
n_train = 100
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
print(trainX.shape, testX.shape)
# fit all models
n_members = 10
members = [fit_model(trainX, trainy) for _ in range(n_members)]
# evaluate different numbers of ensembles on hold out set
single_scores, ensemble_scores = list(), list()
for i in range(1, len(members)+1):
# evaluate model with i members
ensemble_score = evaluate_n_members(members, i, testX, testy)
# evaluate the i'th model standalone
testy_enc = to_categorical(testy)
_, single_score = members[i-1].evaluate(testX, testy_enc, verbose=0)
# summarize this step
print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score))
ensemble_scores.append(ensemble_score)
single_scores.append(single_score)
# summarize average accuracy of a single final model
print('Accuracy %.3f (%.3f)' % (mean(single_scores), std(single_scores)))
# plot score vs number of ensemble members
x_axis = [i for i in range(1, len(members)+1)]
pyplot.plot(x_axis, single_scores, marker='o', linestyle='None')
pyplot.plot(x_axis, ensemble_scores, marker='o')
pyplot.show()
Running the example first reports the performance of each single model as well as the model averaging ensemble of a given size with 1, 2, 3, etc. members.
Your results will vary given the stochastic nature of the training algorithm.
On this run, the average performance of the single models is reported at about 80.4% and we can see that an ensemble with between five and nine members will achieve a performance between 80.8% and 81%. As expected, the performance of a modest-sized model averaging ensemble out-performs the performance of a randomly selected single model on average.
(100, 2) (1000, 2) > 1: single=0.803, ensemble=0.803 > 2: single=0.805, ensemble=0.808 > 3: single=0.798, ensemble=0.805 > 4: single=0.809, ensemble=0.809 > 5: single=0.808, ensemble=0.811 > 6: single=0.805, ensemble=0.808 > 7: single=0.805, ensemble=0.808 > 8: single=0.804, ensemble=0.809 > 9: single=0.810, ensemble=0.810 > 10: single=0.794, ensemble=0.808 Accuracy 0.804 (0.005)
Next, a graph is created comparing the accuracy of single models (blue dots) to the model averaging ensemble of increasing size (orange line).
On this run, the orange line of the ensembles clearly shows better or comparable performance (if dots are hidden) than the single models.
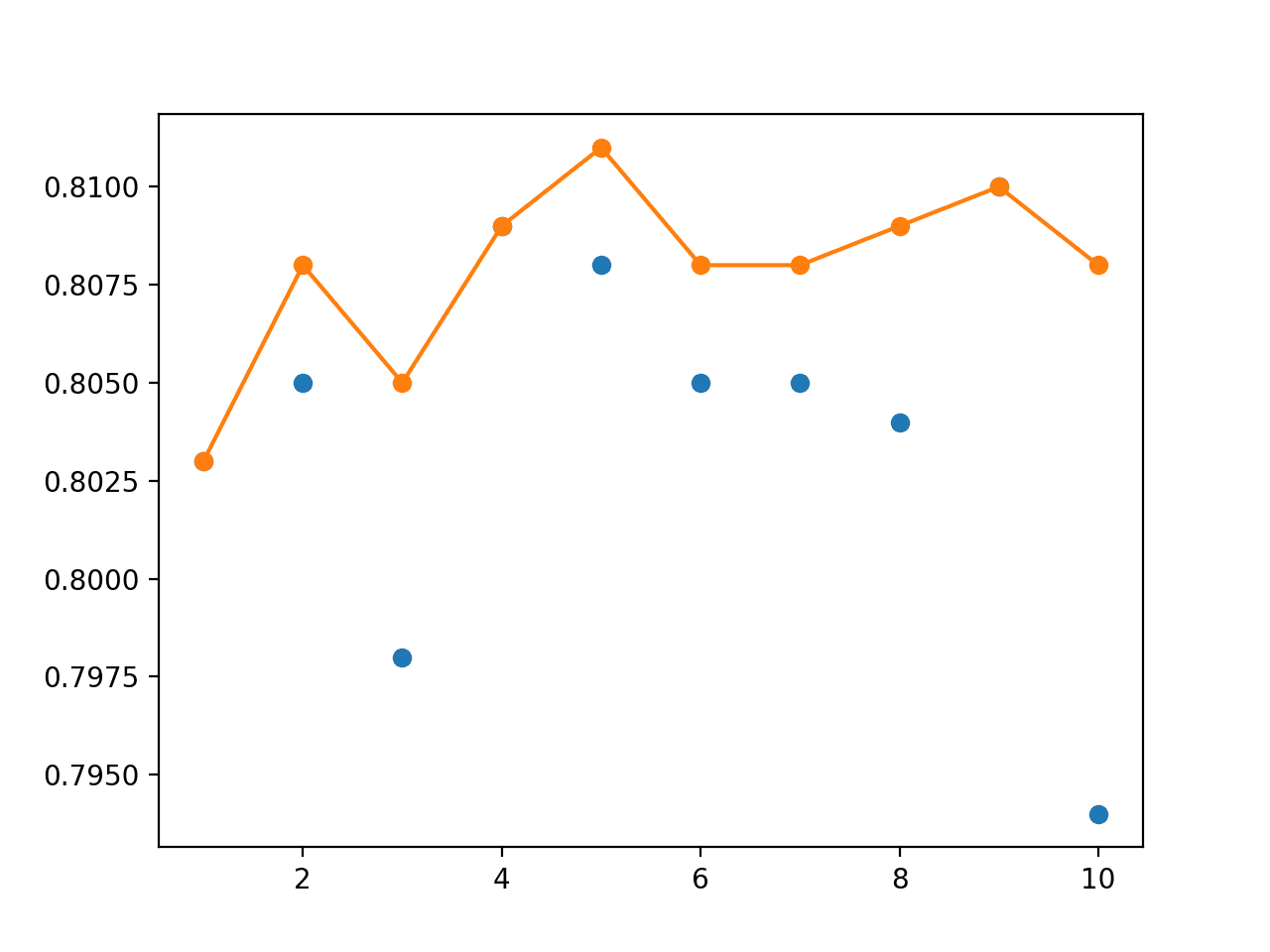
Line Plot Showing Single Model Accuracy (blue dots) and Accuracy of Ensembles of Increasing Size (orange line)
Now that we know how to develop a model averaging ensemble, we can extend the approach one step further by weighting the contributions of the ensemble members.
Grid Search Weighted Average Ensemble
The model averaging ensemble allows each ensemble member to contribute an equal amount to the prediction of the ensemble.
We can update the example so that instead, the contribution of each ensemble member is weighted by a coefficient that indicates the trust or expected performance of the model. Weight values are small values between 0 and 1 and are treated like a percentage, such that the weights across all ensemble members sum to one.
First, we must update the ensemble_predictions() function to make use of a vector of weights for each ensemble member.
Instead of simply summing the predictions across each ensemble member, we must calculate a weighted sum. We can implement this manually using for loops, but this is terribly inefficient; for example:
# calculated a weighted sum of predictions
def weighted_sum(weights, yhats):
rows = list()
for j in range(yhats.shape[1]):
# enumerate values
row = list()
for k in range(yhats.shape[2]):
# enumerate members
value = 0.0
for i in range(yhats.shape[0]):
value += weights[i] * yhats[i,j,k]
row.append(value)
rows.append(row)
return array(rows)
Instead, we can use efficient NumPy functions to implement the weighted sum such as einsum() or tensordot().
Full discussion of these functions is a little out of scope so please refer to the API documentation for more information on how to use these functions as they are challenging if you are new to linear algebra and/or NumPy. We will use tensordot() function to apply the tensor product with the required summing; the updated ensemble_predictions() function is listed below.
# make an ensemble prediction for multi-class classification
def ensemble_predictions(members, weights, testX):
# make predictions
yhats = [model.predict(testX) for model in members]
yhats = array(yhats)
# weighted sum across ensemble members
summed = tensordot(yhats, weights, axes=((0),(0)))
# argmax across classes
result = argmax(summed, axis=1)
return result
Next, we must update evaluate_ensemble() to pass along the weights when making the prediction for the ensemble.
# evaluate a specific number of members in an ensemble
def evaluate_ensemble(members, weights, testX, testy):
# make prediction
yhat = ensemble_predictions(members, weights, testX)
# calculate accuracy
return accuracy_score(testy, yhat)
We will use a modest-sized ensemble of five members, that appeared to perform well in the model averaging ensemble.
# fit all models n_members = 5 members = [fit_model(trainX, trainy) for _ in range(n_members)]
We can then estimate the performance of each individual model on the test dataset as a reference.
# evaluate each single model on the test set
testy_enc = to_categorical(testy)
for i in range(n_members):
_, test_acc = members[i].evaluate(testX, testy_enc, verbose=0)
print('Model %d: %.3f' % (i+1, test_acc))
Next, we can use a weight of 1/5 or 0.2 for each of the five ensemble members and use the new functions to estimate the performance of a model averaging ensemble, a so-called equal-weight ensemble.
We would expect this ensemble to perform as well or better than any single model.
# evaluate averaging ensemble (equal weights)
weights = [1.0/n_members for _ in range(n_members)]
score = evaluate_ensemble(members, weights, testX, testy)
print('Equal Weights Score: %.3f' % score)
Finally, we can develop a weighted average ensemble.
A simple, but exhaustive approach to finding weights for the ensemble members is to grid search values. We can define a course grid of weight values from 0.0 to 1.0 in steps of 0.1, then generate all possible five-element vectors with those values. Generating all possible combinations is called a Cartesian product, which can be implemented in Python using the itertools.product() function from the standard library.
A limitation of this approach is that the vectors of weights will not sum to one (called the unit norm), as required. We can force reach generated weight vector to have a unit norm by calculating the sum of the absolute weight values (called the L1 norm) and dividing each weight by that value. The normalize() function below implements this hack.
# normalize a vector to have unit norm
def normalize(weights):
# calculate l1 vector norm
result = norm(weights, 1)
# check for a vector of all zeros
if result == 0.0:
return weights
# return normalized vector (unit norm)
return weights / result
We can now enumerate each weight vector generated by the Cartesian product, normalize it, and evaluate it by making a prediction and keeping the best to be used in our final weight averaging ensemble.
# grid search weights
def grid_search(members, testX, testy):
# define weights to consider
w = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
best_score, best_weights = 0.0, None
# iterate all possible combinations (cartesian product)
for weights in product(w, repeat=len(members)):
# skip if all weights are equal
if len(set(weights)) == 1:
continue
# hack, normalize weight vector
weights = normalize(weights)
# evaluate weights
score = evaluate_ensemble(members, weights, testX, testy)
if score > best_score:
best_score, best_weights = score, weights
print('>%s %.3f' % (best_weights, best_score))
return list(best_weights)
Once discovered, we can report the performance of our weight average ensemble on the test dataset, which we would expect to be better than the best single model and ideally better than the model averaging ensemble.
# grid search weights
weights = grid_search(members, testX, testy)
score = evaluate_ensemble(members, weights, testX, testy)
print('Grid Search Weights: %s, Score: %.3f' % (weights, score))
The complete example is listed below.
# grid search for coefficients in a weighted average ensemble for the blobs problem
from sklearn.datasets.samples_generator import make_blobs
from sklearn.metrics import accuracy_score
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense
from matplotlib import pyplot
from numpy import mean
from numpy import std
from numpy import array
from numpy import argmax
from numpy import tensordot
from numpy.linalg import norm
from itertools import product
# fit model on dataset
def fit_model(trainX, trainy):
trainy_enc = to_categorical(trainy)
# define model
model = Sequential()
model.add(Dense(25, input_dim=2, activation='relu'))
model.add(Dense(3, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
model.fit(trainX, trainy_enc, epochs=500, verbose=0)
return model
# make an ensemble prediction for multi-class classification
def ensemble_predictions(members, weights, testX):
# make predictions
yhats = [model.predict(testX) for model in members]
yhats = array(yhats)
# weighted sum across ensemble members
summed = tensordot(yhats, weights, axes=((0),(0)))
# argmax across classes
result = argmax(summed, axis=1)
return result
# evaluate a specific number of members in an ensemble
def evaluate_ensemble(members, weights, testX, testy):
# make prediction
yhat = ensemble_predictions(members, weights, testX)
# calculate accuracy
return accuracy_score(testy, yhat)
# normalize a vector to have unit norm
def normalize(weights):
# calculate l1 vector norm
result = norm(weights, 1)
# check for a vector of all zeros
if result == 0.0:
return weights
# return normalized vector (unit norm)
return weights / result
# grid search weights
def grid_search(members, testX, testy):
# define weights to consider
w = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
best_score, best_weights = 0.0, None
# iterate all possible combinations (cartesian product)
for weights in product(w, repeat=len(members)):
# skip if all weights are equal
if len(set(weights)) == 1:
continue
# hack, normalize weight vector
weights = normalize(weights)
# evaluate weights
score = evaluate_ensemble(members, weights, testX, testy)
if score > best_score:
best_score, best_weights = score, weights
print('>%s %.3f' % (best_weights, best_score))
return list(best_weights)
# generate 2d classification dataset
X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2)
# split into train and test
n_train = 100
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
print(trainX.shape, testX.shape)
# fit all models
n_members = 5
members = [fit_model(trainX, trainy) for _ in range(n_members)]
# evaluate each single model on the test set
testy_enc = to_categorical(testy)
for i in range(n_members):
_, test_acc = members[i].evaluate(testX, testy_enc, verbose=0)
print('Model %d: %.3f' % (i+1, test_acc))
# evaluate averaging ensemble (equal weights)
weights = [1.0/n_members for _ in range(n_members)]
score = evaluate_ensemble(members, weights, testX, testy)
print('Equal Weights Score: %.3f' % score)
# grid search weights
weights = grid_search(members, testX, testy)
score = evaluate_ensemble(members, weights, testX, testy)
print('Grid Search Weights: %s, Score: %.3f' % (weights, score))
Running the example first creates the five single models and evaluates their performance on the test dataset.
Your specific results will vary given the stochastic nature of the learning algorithm.
On this run, we can see that model 2 has the best solo performance of about 81.7% accuracy.
Next, a model averaging ensemble is created with a performance of about 80.7%, which is reasonable compared to most of the models, but not all.
(100, 2) (1000, 2) Model 1: 0.798 Model 2: 0.817 Model 3: 0.798 Model 4: 0.806 Model 5: 0.810 Equal Weights Score: 0.807
Next, the grid search is performed. It is pretty slow and may take about twenty minutes on modern hardware. The process could easily be made parallel using libraries such as Joblib.
Each time a new top performing set of weights is discovered, it is reported along with its performance on the test dataset. We can see that during the run, the process discovered that using model 2 alone resulted in a good performance, until it was replaced with something better.
We can see that the best performance was achieved on this run using the weights that focus only on the first and second models with the accuracy of 81.8% on the test dataset. This out-performs both the single models and the model averaging ensemble on the same dataset.
>[0. 0. 0. 0. 1.] 0.810 >[0. 0. 0. 0.5 0.5] 0.814 >[0. 0. 0. 0.33333333 0.66666667] 0.815 >[0. 1. 0. 0. 0.] 0.817 >[0.23076923 0.76923077 0. 0. 0. ] 0.818 Grid Search Weights: [0.23076923076923075, 0.7692307692307692, 0.0, 0.0, 0.0], Score: 0.818
An alternate approach to finding weights would be a random search, which has been shown to be effective more generally for model hyperparameter tuning.
Weighted Average MLP Ensemble
An alternative to searching for weight values is to use a directed optimization process.
Optimization is a search process, but instead of sampling the space of possible solutions randomly or exhaustively, the search process uses any available information to make the next step in the search, such as toward a set of weights that has lower error.
The SciPy library offers many excellent optimization algorithms, including local and global search methods.
SciPy provides an implementation of the Differential Evolution method. This is one of the few stochastic global search algorithms that “just works” for function optimization with continuous inputs, and it works well.
The differential_evolution() SciPy function requires that function is specified to evaluate a set of weights and return a score to be minimized. We can minimize the classification error (1 – accuracy).
As with the grid search, we most normalize the weight vector before we evaluate it. The loss_function() function below will be used as the evaluation function during the optimization process.
# loss function for optimization process, designed to be minimized
def loss_function(weights, members, testX, testy):
# normalize weights
normalized = normalize(weights)
# calculate error rate
return 1.0 - evaluate_ensemble(members, normalized, testX, testy)
We must also specify the bounds of the optimization process. We can define the bounds as a five-dimensional hypercube (e.g. 5 weights for the 5 ensemble members) with values between 0.0 and 1.0.
# define bounds on each weight bound_w = [(0.0, 1.0) for _ in range(n_members)]
Our loss function requires three parameters in addition to the weights, which we will provide as a tuple to then be passed along to the call to the loss_function() each time a set of weights is evaluated.
# arguments to the loss function search_arg = (members, testX, testy)
We can now call our optimization process.
We will limit the total number of iterations of the algorithms to 1,000, and use a smaller than default tolerance to detect if the search process has converged.
# global optimization of ensemble weights result = differential_evolution(loss_function, bound_w, search_arg, maxiter=1000, tol=1e-7)
The result of the call to differential_evolution() is a dictionary that contains all kinds of information about the search.
Importantly, the ‘x‘ key contains the optimal set of weights found during the search. We can retrieve the best set of weights, then report them and their performance on the test set when used in a weighted ensemble.
# get the chosen weights
weights = normalize(result['x'])
print('Optimized Weights: %s' % weights)
# evaluate chosen weights
score = evaluate_ensemble(members, weights, testX, testy)
print('Optimized Weights Score: %.3f' % score)
Tying all of this together, the complete example is listed below.
# global optimization to find coefficients for weighted ensemble on blobs problem
from sklearn.datasets.samples_generator import make_blobs
from sklearn.metrics import accuracy_score
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense
from matplotlib import pyplot
from numpy import mean
from numpy import std
from numpy import array
from numpy import argmax
from numpy import tensordot
from numpy.linalg import norm
from scipy.optimize import differential_evolution
# fit model on dataset
def fit_model(trainX, trainy):
trainy_enc = to_categorical(trainy)
# define model
model = Sequential()
model.add(Dense(25, input_dim=2, activation='relu'))
model.add(Dense(3, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
model.fit(trainX, trainy_enc, epochs=500, verbose=0)
return model
# make an ensemble prediction for multi-class classification
def ensemble_predictions(members, weights, testX):
# make predictions
yhats = [model.predict(testX) for model in members]
yhats = array(yhats)
# weighted sum across ensemble members
summed = tensordot(yhats, weights, axes=((0),(0)))
# argmax across classes
result = argmax(summed, axis=1)
return result
# # evaluate a specific number of members in an ensemble
def evaluate_ensemble(members, weights, testX, testy):
# make prediction
yhat = ensemble_predictions(members, weights, testX)
# calculate accuracy
return accuracy_score(testy, yhat)
# normalize a vector to have unit norm
def normalize(weights):
# calculate l1 vector norm
result = norm(weights, 1)
# check for a vector of all zeros
if result == 0.0:
return weights
# return normalized vector (unit norm)
return weights / result
# loss function for optimization process, designed to be minimized
def loss_function(weights, members, testX, testy):
# normalize weights
normalized = normalize(weights)
# calculate error rate
return 1.0 - evaluate_ensemble(members, normalized, testX, testy)
# generate 2d classification dataset
X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2)
# split into train and test
n_train = 100
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
print(trainX.shape, testX.shape)
# fit all models
n_members = 5
members = [fit_model(trainX, trainy) for _ in range(n_members)]
# evaluate each single model on the test set
testy_enc = to_categorical(testy)
for i in range(n_members):
_, test_acc = members[i].evaluate(testX, testy_enc, verbose=0)
print('Model %d: %.3f' % (i+1, test_acc))
# evaluate averaging ensemble (equal weights)
weights = [1.0/n_members for _ in range(n_members)]
score = evaluate_ensemble(members, weights, testX, testy)
print('Equal Weights Score: %.3f' % score)
# define bounds on each weight
bound_w = [(0.0, 1.0) for _ in range(n_members)]
# arguments to the loss function
search_arg = (members, testX, testy)
# global optimization of ensemble weights
result = differential_evolution(loss_function, bound_w, search_arg, maxiter=1000, tol=1e-7)
# get the chosen weights
weights = normalize(result['x'])
print('Optimized Weights: %s' % weights)
# evaluate chosen weights
score = evaluate_ensemble(members, weights, testX, testy)
print('Optimized Weights Score: %.3f' % score)
Running the example first creates five single models and evaluates the performance of each on the test dataset.
Your specific results will vary given the stochastic nature of the learning algorithm.
We can see on this run that models 3 and 4 both perform best with an accuracy of about 82.2%.
Next, a model averaging ensemble with all five members is evaluated on the test set reporting an accuracy of 81.8%, which is better than some, but not all, single models.
(100, 2) (1000, 2) Model 1: 0.814 Model 2: 0.811 Model 3: 0.822 Model 4: 0.822 Model 5: 0.809 Equal Weights Score: 0.818
The optimization process is relatively quick.
We can see that the process found a set of weights that pays most attention to models 3 and 4, and spreads the remaining attention out among the other models, achieving an accuracy of about 82.4%, out-performing the model averaging ensemble and individual models.
Optimized Weights: [0.1660322 0.09652591 0.33991854 0.34540932 0.05211403] Optimized Weights Score: 0.824
It is important to note that in these examples, we have treated the test dataset as though it were a validation dataset. This was done to keep the examples focused and technically simpler. In practice, the choice and tuning of the weights for the ensemble would be chosen by a validation dataset, and single models, model averaging ensembles, and weighted ensembles would be compared on a separate test set.
Extensions
This section lists some ideas for extending the tutorial that you may wish to explore.
- Parallelize Grid Search. Update the grid search example to use the Joblib library to parallelize weight evaluation.
- Implement Random Search. Update the grid search example to use a random search of weight coefficients.
- Try a Local Search. Try a local search procedure provided by the SciPy library instead of the global search and compare performance.
- Repeat Global Optimization. Repeat the global optimization procedure multiple times for a given set of models to see if differing sets of weights can be found across the runs.
If you explore any of these extensions, I’d love to know.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
- When Networks Disagree: Ensemble Methods for Hybrid Neural Networks, 1995.
- Neural Network Ensembles, Cross Validation, and Active Learning, 1995.
- Learning with ensembles: How over-fitting can be useful, 1996.
API
- Getting started with the Keras Sequential model
- Keras Core Layers API
- scipy.stats.mode API
- numpy.argmax API
- sklearn.datasets.make_blobs API
- numpy.argmax API
- numpy.einsum API
- numpy.tensordot API
- itertools.product API
- scipy.optimize API
- scipy.optimize.differential_evolution API
Articles
- Ensemble averaging (machine learning), Wikipedia.
- Cartesian product, Wikipedia.
- Implementing a Weighted Majority Rule Ensemble Classifier, 2015.
- Example of weighted ensemble, Kaggle Kernel.
- Finding Ensemble Weights, Kaggle Kernel.
Summary
In this tutorial, you discovered how to develop a weighted average ensemble of deep learning neural network models in Python with Keras.
Specifically, you learned:
- Model averaging ensembles are limited because they require that each ensemble member contribute equally to predictions.
- Weighted average ensembles allow the contribution of each ensemble member to a prediction to be weighted proportionally to the trust or performance of the member on a holdout dataset.
- How to implement a weighted average ensemble in Keras and compare results to a model averaging ensemble and standalone models.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
The post How to Develop a Weighted Average Ensemble for Deep Learning Neural Networks appeared first on Machine Learning Mastery.
Machine Learning Mastery published first on Machine Learning Mastery
No comments:
Post a Comment